JaeHyeonKim19

본 글은 영남대학교 최규상 교수님의 컴퓨터 구조 강의를 듣고 작성된 글입니다.

3.1 Introduction

3.2 Addition and Subtraction

• Integer Addition

  • Overflow if result out of range

    • Adding +ve and -ve operands, no overflow

    • Adding two +ve operands

      • Overflow if result sign is 1
    • Adding tow -ve operands -Overflow if result sign is 0

• Integer Subtraction

  • Add negation of second operand

  • Overflow is result out of range

    • Subtracting two +ve or two -ve operands, no overflow

    • Subtracting +ve from -ve operand

      • Overflow if result sign is 0

    • Subtracting -ve from +ve operand

      • Overflow if result sign is 1

• Dealing with Overflow

  • Some languages(e.g., C) ignore overflow

    • Use MIPS addu, addui, subu instructions
  • Other languages(e.g., Ada, Fortran) require raising an exception

• Arithmetic for Multimedia

  • Graphics and media processing operates on vectors of 8-bit and 16-bit data

    • Use 64-bit adder, with partitioned carry chain

      • Operate on 8*8-bit, 4*16-bit, or 2*32-bit vectors
      • SIMD (single-instruction, multiple-data)

  • Saturating operations

    • On overflow, result is larges representable value
    • E.g., clipping in audio, saturation in video

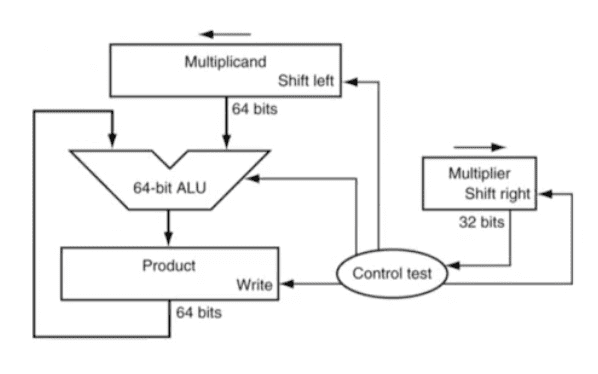
3.3 Multiplication

3.4 Division

3.5 Floating Point

• Representation for non-integral numbers

  • Including very small and very large numbers

• Like scientific notation

  • normalized

    • -2.34 * 10^56

  • not normalized

    • +0.002 * 10^-4
    • +987.02 * 10^9

• In binary

  • +-1.xxxxx * 2^n
• Types float and double in C

• Floating Point Standard

  • Defined by IEEE Std 754-1985

  • Developed in response to divergence of representations

    • Portability issues for scientific code
  • Now almost universally adopted

  • Two representations

    • Single precision (32-bit)

      • sign: 1 bit
      • exponent: 8 bit
      • fraction: 23 bit

    • Double precision (64-bit)

      • sign: 1bit
      • exponent: 11 bit
      • fraction: 52 bit

• IEEE Floating-Point Format

  • x = (-1)^S * (1 + Fraction) * 2^(Exponent - Bias)

  • S: sign bit

    • 0: non-negative
    • 1: negative

  • Normalize significand: 1.0 <= |significand| < 2.0

    • Always has a leading pre-binary-point 1 bit, so no need to represent if explicitly (hidden bit)
    • Significand is Fraction with the "1." restored

  • Exponent: excess representation: actual exponent + Bias

    • Ensures exponent is unsigned
    • Single: Bias = 127; Double: Bias = 1203

• Infinities and NaNs

  • Exponent = 111...1, Fraction = 000...0

    • +-Infinity
    • Can be used in subsequent calculations, avoiding need for overflow check

  • Exponent = 111...1, Fraction != 000...0

    • Not-a-Number (NaN)

• Floating-Point Addition

  1. Align binary points
  2. Add significands
  3. Normalize result & check for over/underflow
  4. Round and renormalize if necessary

• Floating-Point Adder Hardware

  • Much more complex than integer adder

  • Doing it in one clock cycle would take too long

    • Much longer than integer operations
    • Slower clock would penalize all instructions

  • FP adder usually takes several cycles

    • Can be pipelined

• Floating-Point Multiplication

  1. Add exponents
  2. Multiply significands
  3. Normalize result & check for over/underflow
  4. Round and renormailze if necessary
  5. Determine sign

• Floating-Point Arithmetic Hardware

  • FP multiplier is of similar complexity to FP adder

  • FP arithmetic hardware usually does

    • Addition, subtraction, multiplication division, reciprocal, square-root
    • FP <-> integer conversion

  • FP adder usually takes several cycles

    • Can be pipelined